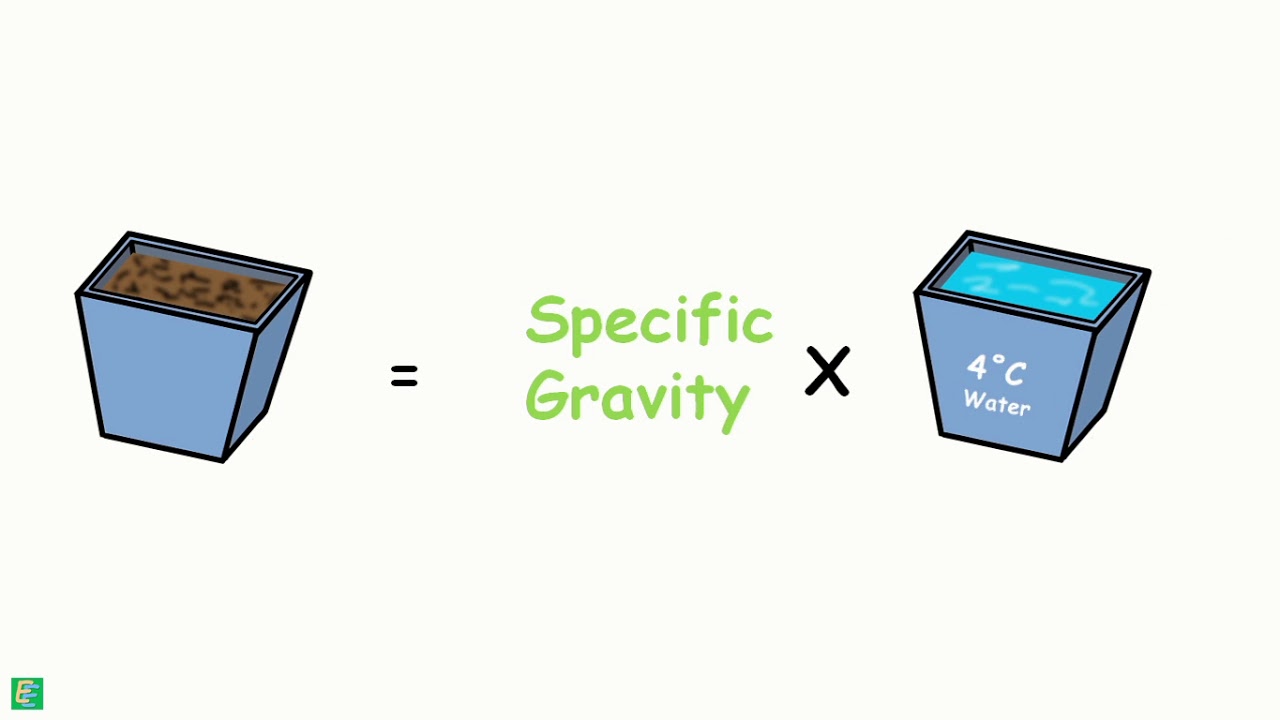
Soil particles in a soil mass experience weight of everything above them which includes weight of all the soil particles above them, weight of water and weight of structure if present, and because of that soil particles experience stress in between each other which we call total stress.

But if we put this soil mass in water then because of buoyancy force the net total downward force is reduced consequently the stress on particles is reduced. This reduced stress is called effective stress.

The stress exerted by the water present in the soil pores is called the pore water pressure.

 

We can write expression for effective stress as this

 

Effective stress is also represented as σ'.

Effective stress is different at different depths below ground surface because total stress and pore water pressure changes at different depth.

We will try to calculate the effective stress at different plane sections in the soil while considering different water table levels.

 

If level of water table in the soil changes because of any external factors like rain or increased overburden pressure, the movement of water takes place inside the voids present in the soil mass. This state of movement of water inside the soil is called the hydro dynamic state or transient state of water.

 

For now we will discuss only hydrostatic conditions when no movement of water takes place in the voids.

 

 

So lets us consider this soil mass in which the position of the water table is H₁ depth below the ground surface.

 

Soil below the ground water table is fully saturated and has unit weight γ_sat, while soil above the water table may not be completely dry hence its unit weight is considered bulk unit weight γ.

We will try to find out the effective stress at the point or plane within the saturated layer under the soil.

 

Stress at any point or plane under the soil can be given as force on that plane divided by the area of the plane.

 

Force on that plane is the weight of soil above the plane and that is unit weight of soil multiplied by its volume. Volume is area multiplied by the height of the soil mass.

 

This can be simplified to this:

σ  = γH

 

Hence we can directly write the stress under any material as its unit weight multiplied by the height of the material above that point.

 

So on a plane that lies within the saturated layer of the soil deposit total downward stress is equal to the stress because of soil and water above it. Depth of unsaturated soil layer is assumed H₁ and let the plane where we are calculating the stress is at depth H₂ from the water table.

 

Hence total stress on this plane because of this not-saturated soil mass is γH₁ and stress due to saturated soil mass is γ_satH₂.

σ = γH₁ + γ_satH₂

 

We should note here that gamma sat already includes the weight of the water present in the soil mass.

Now the pore water pressure at this plane is because of water present above this plane up to the height of H₂. So pore water pressure on this plane is

u = γ_wH₂

 

Hence we can calculate the effective stress on this plane in the soil as

σ' = σ − u

 

By writing the corresponding values we get this:

σ' = (γH₁ + γ_satH₂) - (γ_wH₂)

 

and by rearranging it we can also write it as this:

σ' = γH₁ + (γ_sat - γ_w)H₂

 

if we remember, the quantity in the bracket is called submerged unit weight. so we can write this expression as :

σ' = γH₁ + γ’H₂

γ’ is the submerged unit weight of soil.

So this is the expression for the effective stress on this plane in the soil.

 

 

Now if the water table rises to the ground, the whole soil deposit becomes completely saturated.

 

Total stress at this plane is now caused by the whole saturated soil mass which we can write as saturated unit weight of soil multiplied by the total height of the soil mass.

σ = γ_sat(H₁ +H₂)

 

Pore water pressure here becomes unit weight of water multiplied by soil deposit height.

u = γ_w(H₁ +H₂)

 

Hence effective stress can be calculated as this.

σ' = σ − u

σ' = γ_sat(H₁ +H₂) - γ_w(H₁ +H₂)

σ’ = (γ_sat - γ_w)(H₁ +H₂)

 

We write this as submerged unit weight of soil

σ’ = γ’(H₁ +H₂)

 

We know that submerged unit weight of soil γ’ is less than bulk unit weight γ because of the buoyancy factor. So here if we compare the result we obtained in saturated soil mass with the result we obtained in partially saturated soil condition, we can note that because of the rise in the water table the effective stress on the particles at a particular depth decreases.

 

In another case if the water table falls below our observation plane then pore water pressure becomes zero, as no water present in the voids to apply pressure.

 

Effective stress will be the total stress which is the bulk unit weight of the soil multiplied by height of the soil mass.

σ' = σ = γ(H₁ +H₂)

 

Again if we compare this result with the result of the initial partially saturated condition, we observe because of the water drawdown the effective stress has increased.

 

 

Now consider a different soil condition where soil mass consists of two different soil deposits which have different bulk unit weights γ₁ and γ₂.

We will calculate the values of effective stress at different sections of this soil deposit with different hydrostatic conditions.

 

Let’s begin by imagining the water table is above the soil mass and is of height H_O. These soils become saturated and their bulk unit weights become γ_sat1 and γ_sat2. Thickness of top layer is H₁ and bottom layer is H₂.

 

We start calculating the effective stress on a plane section at the surface of the soil.

On this plane the downward stress is caused by the weight of above material which here is water only. So, total stress on this plane is unit weight of water multiplied by the height of the water layer above this plane section.

σ = γ_wH_O

 

Now the pore water pressure on this plane caused by the water above is unit weight of water multiplied by the height of the water.

u = γ_wH_O

 

Hence effective stress on this plane is

σ’ = σ – u

σ’ = γ_wH_O – γ_wH_O

 

both are equal so effective stress is zero.

σ’ = 0

 

We can also visualize this situation, as we know that effective stress is the stress transferred at the contact of soil particles, but in our example above our plane of consideration there are no soil particles present. So no inter-particle force transfer, hence effective stress on this plane is zero.

 

 

Now move down a little and let us calculate the effective stress on a plane section within the top soil layer, which is H₁’ depth below the actual soil surface.

 

Total stress on this plane section is caused by the above water layer and this soil mass. Stress caused by water layer is γ_wH_O and stress caused by the saturated soil layer above the plane is γ_(sat)1H₁’.

σ = γ_wH_O + γ_(sat)1H₁’

 

We should again keep in mind that water present in the soil voids will also cause to generate the vertical downward stress on the plane because of its weight, but in the calculation of total stress we have taken the saturated unit weight of the soil that includes the weight soil particles and weight of water as well.

 

Now pore water pressure at this plane is because of the whole water available above this plane. Which is γ_w multiplied by whole height of water surface.

u = γ_w(H_O+ H₁’)

 

Hence effective stress can be calculated as

σ’ = σ – u

σ’ = (γ_wH_O + γ_(sat)1H₁’) - (γ_wH_O+ γ_wH₁’)

σ’ = (γ_(sat)1 - γ_w)H₁’

 

it can be written as this :

σ’ = γ’H₁’

 

If we need to calculate the effective stress at the plane, where the two soil layers meet each other, the expression for effective stress will remain the same and only the depth of our observation plane from the soil surface, which is the only variable here, changes to H₁, which is now the depth of our new observation plane from the soil surface.

σ’ = γ’H₁

 

 

Now let’s move downwards a little more and calculate the effective stress on a plane somewhere in the middle of bottom soil layer. Let’s say the depth of the observation plane in the bottom layer is H₂’.

 

total stress on this plane is stress due to the top water layer γ_wH_O, stress due to the saturated top soil layer γ_(sat)1H₁, and stress due to saturated bottom soil layer above plane γ_(sat)2H₂’.

σ = γ_wH_O + γ_(sat)1H₁ + γ_(sat)2H₂’

 

pore water pressure on this plane is γ_w multiplied by total height of the water above the plane

u = γ_w(H_O + H₁ + H₂’)

 

So effective stress can be calculated as this

σ’ = σ – u

σ’ = (γ_wH_O + γ_(sat)1H₁ + γ_(sat)2H₂’) - (γ_wH_O + γ_wH₁ + γ_wH₂’)

= (γ_(sat)1 - γ_w)H₁- (γ_(sat)2 - γ_w)H₂’

 

which can be written as

σ’ = γ₁’H₁- γ₂’H₂’

 

If we need to calculate the effective stress at the bottom of the bottom soil layer, the expression for effective stress will again remain the same and only the depth of our observation plane H₂’, which is the only variable here, changes to the thickness of the soil layer H₂.

σ’ = γ₁’H₁- γ₂’H₂

 

 

Hence with all our calculations we observed that change in the water level above the ground does have no effect on effective stress and it remains unchanged. As we can see the height of the water above the surface is not in any equation, because increased height of the water above the ground level causes to increase in the total stress as well as the pore water pressure.

 

 

Now let’s discuss the case when water level has dropped to the soil surface.

 

Of course the plane section at the surface has nothing above it and total stress is zero and so is the pore water pressure. Consequently effective stress at this section is zero.

σ’ = σ – u

σ’ = 0 – 0 = 0

 

Now let us calculate the effective stress on the plane where these soils meet each other. We can also take this plane anywhere in the top soil layer but result will be similar and only the depth of the observation will change.

 

Total stress on this plane due to saturated soil layer above, γ_(sat)1H₁.

σ = γ_(sat)1H₁

 

and pore water pressure is γ_wH₁

u = γ_wH₁

 

hence effective stress will be

σ’ = σ – u

σ’ = (γ_(sat)1H₁) - (γ_wH₁)

σ’ = (γ_(sat)1 - γ_w)H₁

 

and this can be written as this :

σ’ = γ’₁H₁

 

 

Now on the plane section at the bottom of soil deposit

 

the total stress is due to saturated soil layers above the plane is

σ = γ_(sat)1H₁ + γ_(sat)2H₂

 

Pore water pressure at this plane is

u = γ_wH₁ + γ_wH₂

 

Hence effective stress will be

σ’ = σ – u

σ’ = (γ_(sat)1H₁ + γ_(sat)2H₂) - (γ_wH₁+ γ_wH₂)

σ’ = (γ_(sat)1 - γ_w)H₁ + (γ_(sat)2 - γ_w)H₂

 

Which we write in submerged unit weight of soils as this.

σ’ = γ₁’H₁ + γ₂’H₂

 

 

Now water level in the soil has dropped and water table is now somewhere within the top layer of the soil mass. Again we will calculate the effective stress on these different sections.

At the top layer as we have already seen there will be no stress and effective stress is zero.

 

Now at the level where soil deposit meet each other:

 

Total stress at this plane is the sum of stress due to the soil above this plane which is both saturated and not saturated. Stress due to not saturated part of soil is bulk unit weight of soil γ₁ multiplied by the height of unsaturated soil, say H₁’, and stress due to saturated part of the soil is γ_(sat)1 multiplied by saturated height of water above the plane, say H₁’’.

 

σ = γ₁H₁’ + γ_(sat)1H₁’’

 

pore water pressure is γ_w and height of the water above plane

u = γ_wH₁’’

 

So effective stress is

σ’ = σ – u

σ’ = (γ₁H₁’ + γ_(sat)1H₁’’) - (γ_wH₁’’)

σ’ = γ₁H₁’ + (γ_(sat)1- γ_w)H₁’’

 

and this can be written in submerged unit weight as this :

σ’ = γ₁H₁’ + γ₁’H₁’’

 

 

Now if we calculate the effective stress at the bottom of the second layer.

 

Total stress at this plane is unit weight of unsaturated soil 1 γ₁H₁’ plus stress due to saturated soil 1 γ_(sat)1H₁’’ plus stress due to the whole saturated bottom soil layer γ_(sat)2H₂

σ = γ₁H₁’+ γ_(sat)1H₁’’+ γ_(sat)2H₂

 

Pore water pressure will be because of total water layer above

u = γ_wH₁’’ + γ_wH₂

 

Hence effective stress can be calculated as this

σ’ = σ – u

σ’ = (γ₁H₁’+ γ_(sat)1H₁’’+ γ_(sat)2H₂) - (γ_wH₁’’ + γ_wH₂)

σ’ = γ₁H₁’+ (γ_(sat)1 - γ_w)H₁’’ + (γ_(sat)2 - γ_w)H₂

 

Which is also written as this

σ’ = (γ₁H₁’+ γ₁’H₁’’ + γ₂’H₂)

 

 

Now we assume water level has dropped even further and water table is now somewhere within the bottom layer of the soil mass.

 

Effective stress on the surface of the soil deposit will be zero.

 

Now the stress at the plane section where soil deposits meet will only because unsaturated soil layer above.

So total stress, at this plane, is bulk unit weight of soil, γ₁, multiplied by thickness of layer H₁.

σ = γ₁H₁

 

No water is present above this plane so pore water pressure is zero here

u = 0

 

Hence effective stress will be equal to the total stress.

σ' = γH₁ – 0 = γ₁H₁

 

 

Finally we calculate the effective stress at the bottom most plane section.

 

Total stress on the bottom most plane is stress due to top unsaturated soil layer γ₁H₁ plus stress due to unsaturated part of the bottom soil deposit of thickness say H₂’ plus stress due to saturated part of the bottom soil deposit γ_(sat)2H₂’’.

σ = γ₁H₁ + γ₂H₂’ + γ_(sat)2H₂’’

 

here pore water pressure will be

u = γ_wH₂’’

 

So effective stress will be

σ’ = σ – u

σ’ = (γ₁H₁ + γ₂H₂’ + γ_(sat)2H₂’’) – (γ_wH₂’’)

σ’ = γ₁H₁ + γ₂H₂’ + (γ_(sat)2 – γ_w)H₂’’

 

part of the equation can also be written as submerged unit weight of bottom soil layer

σ’ = γ₁H₁ + γ₂H₂’ + γ₂’H₂’’