A soil mass is composed of small solid particles which we call the soil grains. These soil grains when depositing in a soil mass arranges themselves in a way that some amount of empty space is left between them. We call these spaces voids.

And the property of the soil which permits the water or any liquid to flow through it through its voids is called permeability. Permeability is the ease with which water can flow through the soils.

Permeability of the soil in its natural deposits is highly influenced by its natural structural factors such as its non-homogeneity and stratification.

In an inhomogeneous soil deposit water faces different movement resistances when it moves in different directions as the soil has different types of variations in different directions. Consequently we observe different values of permeability in different directions.

Sometimes soil deposits we observe in the field consist of number of different layers stacked one over the other and each layer has different engineering properties and permeability. Such a soil deposits are called stratified soil deposits.

For the measurement of amount of water percolating through these stratified soil deposits we calculate the average value of the coefficient of permeability. For calculations and analysis purpose it is assumed that in stratified soils each individual layer is homogeneous and isotropic. That means each single layer has similar structure and physical properties in all the directions.

The average coefficient of permeability of the whole soil deposit varies with the direction of the flow. So we calculate the permeability of such deposit for flow of water in two directions.

1. Horizontal Flow that is Flow Parallel to Bedding Planes

2. Vertical Flow that is Flow Perpendicular to Bedding Planes

Let’s calculate coefficient of permeability for each one by one.

Horizontal Flow (Flow Parallel to Bedding Planes)

Consider a soil deposit consist these horizontal soil layers of thickness H₁, H₂, H₃ and so on. Permeability of these layers are k₁, k₂, …. up to k_n.

As we have already assumed that each individual soil layer is homogeneous and isotropic so permeability of each layer is same in both horizontal and vertical direction.

When water flows through such soils in parallel or horizontal direction, let’s say head loss which is the energy loss of water is observed h over a distance of L. So it generate the hydraulic gradient i which is h by L.

We can see the head loss is same for all the layers and also the length of flow is same so the hydraulic gradient of total soil mass i will be similar to the hydraulic gradient of each layer.

Hence i = i₁ = i₂ = i₃

When water flows through soil layers in horizontal direction, the water flows in all the layers at the same time. The discharge through each layer is q₁, q₂ and so on.

From the continuity equation we can write the total discharge through soil mass is equal to the sum of discharge through each layer.

q = q₁ + q₂ + q₃ + ………. +q_n

Note this as equation number 1.

From the Darcy’s law we can write discharge through the soil mass is equal to the permeability of the soil multiplied by the area through which water is percolating multiplied by hydraulic gradient which is causing the flow.

q=KAi

Here let’s say total thickness of the soil mass capital H and its width is capital B.

So area of flow is BH. We also write permeability of this whole soil mass in horizontal direction of flow as K_H

So discharge can be written as this.

q=K_H(BH)i

Similarly discharge through first layer can be written as

q₁ = K₁i(BH₁)

Here k₁ is permeability of the first layer which is of thickness H₁

Discharge through second layer is

q₂ = k₂i(BH₂)

And so on..

q... = k_...i(BH_...)

q_n = k_ni(BH_n)

Substitute all these values in equation number one

KiH = k₁i(BH₁) + k₂i(BH₂) + …………….. + k_ni(BH_n)

By simplifying this we can get the permeability value for the stratified soil deposit when the flow of water is in horizontal direction.

Vertical Flow

Now let us consider the same soil deposit, but this time water is flowing vertically downwards.

In this kind of situations the flow takes place in one layer after another. We can observe whatever amount of water is coming out of one layer is going in into another layer. So discharge through each layer will be equal and that will be equal to the discharge through the whole soil mass.

So we can write q = q₁ = q₂ = q_... = q_n

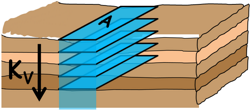
If we assume the area of flow is A which is same for all the layers then we can write by Darcy’s law as

K_vAi = K₁Ai₁ = K₂Ai₂ = K_...Ai_... = K_nAi_n

K_V is the permeability of this whole soil mass in vertical direction of flow.

It may be simplified to

K_vi = K₁i₁ = K₂i₂ = K_...i_... = K_ni_n

From here we can write hydraulic gradient throughout any layer which is causing the flow within a layer as this

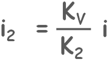
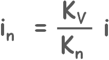
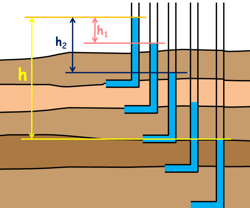Head loss through each layer may be different but total head loss will be equal to the sum of head loss through all the soil layers.

Which we write :

h = h₁ + h₂ + h₃ + h_... + h_n

Here h is the total head loss and h₁ h₂ are head loss of first and second layer respectively.

We know that hydraulic gradient is equal to the head loss divided by the length of the flow.

i = h/L

So head loss can be written as this : h = i x L

L is the length of the flow which in our case is the thickness of the layers as water is flowing vertically downwards.

So we can write total head loss as this

Hi = H₁i₁ + H₂i₂ + ………..+ H_...i_... + H_ni_n

Now we can write values of the hydraulic gradient from equation 1.

By simplifying this we can get the permeability value for the stratified soil deposit when the flow of water is in vertical direction.

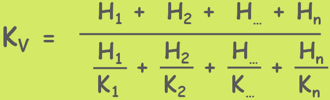
It has been observed that permeability of soil strata in horizontal flow is always found greater than the vertical flow that is K_H is greater than K_V.