A soil mass is composed of small solid particles which we call the soil grains. These soil grains when depositing in a soil mass arranges themselves in a way that some amount of empty space is left between them. We call these empty spaces voids.

 

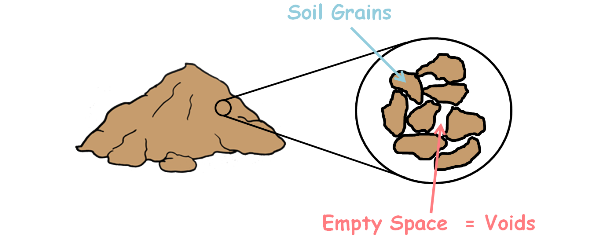
These voids or pores are interconnected and form a highly complex network of irregular tube like structure.

 

When water is subjected to a potential difference in the soil, it flows through these voids from high potential to low potential. The surface of the soil particles offers a resistance to the flow of water. The more irregular and narrower the voids, greater is the resistance posed to the water flowing while more open the voids, greater is the ease with which water flows through soil.

 

This property of the soil which permits the water or any liquid to flow through it through its voids is called permeability. It is the ease with which water can flow through the soils.

Gravel particles are large. Larger the soil grains, larger will be the volume of voids and better will be the connectivity of those pores, consequently large amount of water may flow through them easily and higher will be the flow of water, and that we say higher is the permeability of the soil.

 

A soil has different values of permeability for different liquids but we will focus only on soil’s permeability with water.

 

There is a huge difference in permeability of different soils. These are the values of permeability of different soils.

 

Gravel soils are most permeable while clay soils are least permeable.

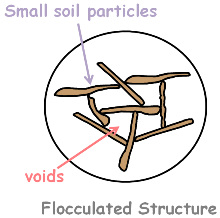
Clay soils have high void ratio as they have large volume of voids because of their flocculated soil structure. These voids in the figure look very large but it is much zoomed view and because of clay particles being very small these voids are poorly connected to each other and do not form a regular tube or channel like structure. Hence even after having large amount of voids the clay soils are very less permeable.

When a soil has extremely low permeability it is termed as impervious soil.

 

 

Water in the soil flows from one point to another only if there is a difference of hydraulic head.

 

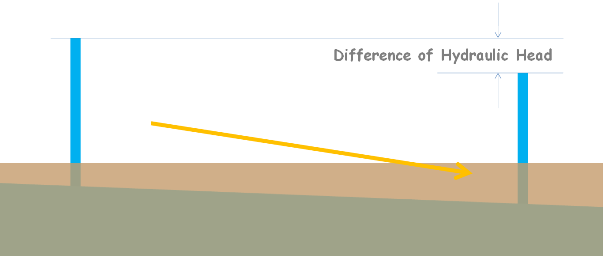
The hydraulic head is the amount of mechanical energy available at any point in water.

 

From Bernoulli's Principle, the total head or total energy at a given point in a fluid is the energy due to the movement of the fluid which we call velocity head, plus energy from the pressure in the fluid which is called pressure head, plus energy from the height of the fluid relative to any arbitrary datum which is called elevation head.

 

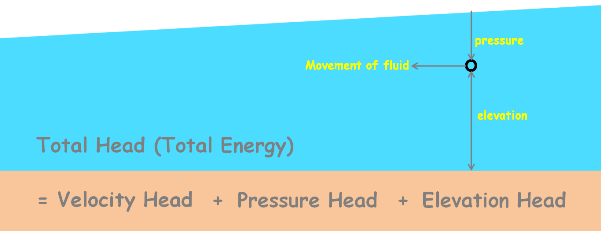
Datum can be understood as any reference line or plane. Here elevation represents the height or elevation of point of consideration from our considered datum.

 

This total head has the unit of height such as meters.

When water flows through the soils its velocity is very small therefore we neglect the velocity head.

 

Water flows from higher energy region to lower energy region. If the hydraulic head of point A is higher than the head of B water may flow from point A to B.

 

Hydraulic Head of point A :

 

Hydraulic Head of point B :

 

Similarly if head of B is higher than head of A water may flow from point B to A.

 

Water does not flow if the point A and B have the same energy or have inadequate head difference because even if A has higher elevation than point B the hydraulic gradient of both the points is same. Because hydraulic gradient which is the sum of both elevation head and pressure head, of both the points is same.

 

Elevation of point A is higher than that of point B. But suppose if point B has high pressure head because of any geological confined aquifer conditions then total head of point B may be higher than that of point A. In that case water will flow from point B to A even against gravity.

 

Note that fluid flows down from high hydraulic head to low hydraulic head.

 

The change in the hydraulic head per unit distance over which this change occurs is called hydraulic gradient.

 

Hydraulic gradient is determined by making several wells at some distances and measuring the water level in them.

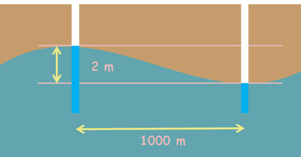
For example to measure the hydraulic gradient of ground water we make two wells in the ground 1000 meters apart and measure the difference of water level in them. If the difference of water level in these two wells is 2 meters, the hydraulic gradient is:

 

 

 

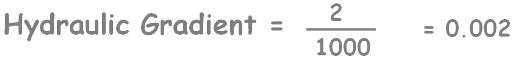
We take a soil sample of length L and having a cross-sectional area of A. We subject it to some hydraulic gradient.

 

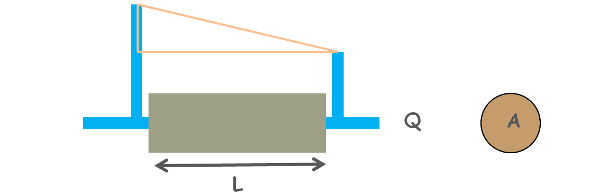
We also measure the output discharge of the water through this soil. We can get the velocity of flow through soil by continuity equation as velocity equal to discharge divided by cross-sectional area of soil.

 

We increase the hydraulic gradient and for different hydraulic gradient values we note down corresponding velocity of water through the soil. We plot a graph between these obtained values of hydraulic gradient applied and velocity of flow. We will notice with the increase in the hydraulic gradient velocity of flow also increases.

 

We can divide this graph into three regions namely zone 1, zone 2 and zone 3

Zone 3, where the curve is irregular, displays turbulent flow of water inside voids.

Zone 1 depicts the laminar flow and zone 2 is transition zone.

 

In laminar flow the particles of water follow a defined path such that the path of one particle never intersects the path of any other particle. While turbulent flow is irregular.

 

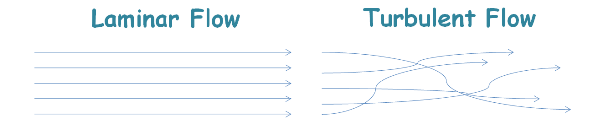
We can observe, in zone 1 hydraulic gradient and velocity of flow share a linear relationship.

This relationship was first observed by French engineer Henry Darcy and proposed what is known as Darcy’s law.

 

He demonstrated after doing experiments that the velocity of flow of liquid between two points in the soil is directly proportional to the hydraulic gradient applied to it.

v α i

 

We can write it as this by adding a proportionality constant k.

v = ki

 

K is the coefficient of Permeability.

v is the velocity of flow which is also known as discharge velocity or superficial velocity

i is hydraulic gradient

 

From this we can write coefficient of permeability as

 

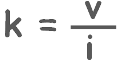
Here if the hydraulic gradient is unity, that is one, the coefficient of permeability will be equal to the velocity of flow.

k = v

In other words, the coefficient of permeability is the velocity of flow of liquid inside the soil if the hydraulic gradient is unity.

 

The coefficient of permeability has the dimensions of velocity, as hydraulic gradient is dimensionless because it is length divided by length.

 

 

Discharge through soil can be written as this

Q = AV

This can be written as this :

q = KAi

or

 

 

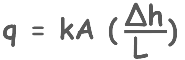
The flow of liquid takes place actually through the soil pores not through the whole cross-sectional area because primarily this cross-sectional area is composed of soil solids and very less area is available for the voids. But for the calculations we have considered the whole soil area.

 

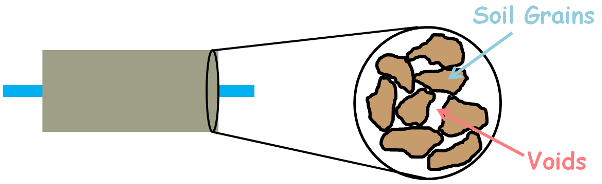
So let’s say average area of voids is As and the flow of water in the soil pores as velocity Vs.

 

Using the continuity equation we can write discharge through whole cross-sectional area is actually equal to the discharge through its voids.

 

We can re-write it for pore velocity.

Now let’s multiply both numerator and denominator by the length of the specimen L. We can see one quantity makes up total volume of soil sample and other one makes total volume of voids.

 

And if we write it as this then we can see denomenator ratio is the porosity of the soil.

 

So we can write this equation as

.

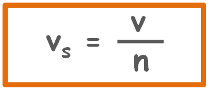
This velocity of liquid through voids is called the seepage velocity.

 

We know that porosity cannot be greater than 1,

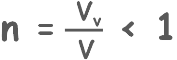
So if porosity is smaller than one then seepage velocity will always be greater than discharge [superficial] velocity.

 

 

Assumptions of Darcy’s law

To apply Darcy’s law we assume that

1. Soil is fully saturated which means all the voids are completely filled with water.

2. The flow is laminar inside the voids. For large soil pores of gravels and at higher hydraulic gradient flow may become turbulent. For that Darcy’s law is invalid.

 

Permeability is useful in many engineering problems such as

1. In an earth dam we may need to estimate the quantity of water leakage through and under it.

 

2. If a foundation is resting on a certain type of soil and because of the overburden pressure if water is escaping out of the soil we may need to know how much time in which settlement will take place. That is rate of the settlement of a foundation or building.

 

3. To keep a toxic liquid in a lagoon we must understand the permeability of the soil that how much liquid will pass through it and how much time it’ll take to contaminate the water table below.

 

Depending upon the work sometimes we need to use soils which restrict the flow of water which are low permeability soils and sometimes we need to use soils which facilitate the flow of water which are high permeability soils.