If you've ever driven or hiked along a mountain road, you've likely seen massive concrete walls holding back tons of earth. Ever wondered why they’re there?

Well, it’s because of the stability of the soil. And Stability of soil depends on the slope of its surface. When the slope is steeper than what’s considered safe, the soil becomes unstable and can collapse. While on the other hand, if the slope is gentle and flatter than the critical angle, it's much safer.

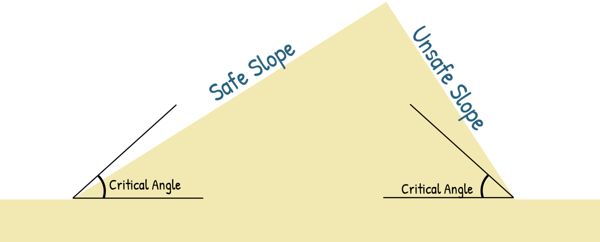
But what if there’s no space to create that gentle slope, and a steeper slope is unavoidable? In such cases, a supporting structure is built to keep the soil in place.

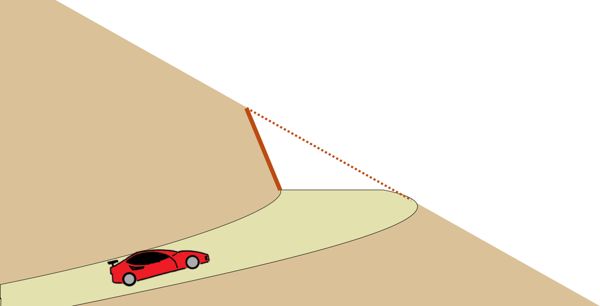
So when the soil needs to be held back at a steep angle, we create these walls—structures designed to provide the lateral support necessary to keep the earth from moving. These structures are called Retaining Walls.

Without a retaining wall, the soil from the steep slope would slide down, making the slope unstable.

The soil that the wall is holding back exerts pressure on the wall, and this pressure is called Earth Pressure. However, the term 'earth pressure' can sometimes cause confusion, as it could refer to either vertical or horizontal or both the forces exerted by the soil. To be more specific, the horizontal force exerted on the wall is called Lateral Earth Pressure.

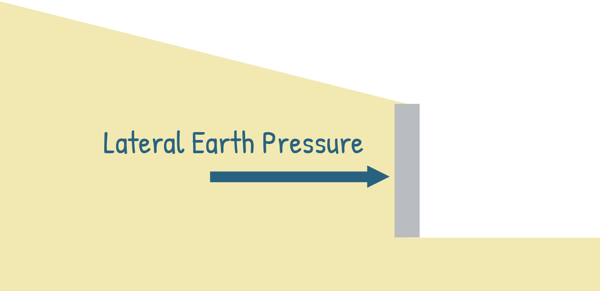
Now, designing a retaining wall isn't as simple as just stacking up concrete. It requires careful calculations of the magnitude — or the amount of force — with which the soil is pushing against the wall, and exactly where that force is acting.

The magnitude of this force depends on a few more factors, like the rigidity or flexibility of the wall, the relative movement of the soil and structure, the type of soil the wall is supporting, and even the drainage conditions around it.

As we can see, there are a lot of factors at play here. And because of that, determining earth pressure isn’t always straightforward — it’s often statically indeterminate, meaning there’s no single, direct equation to solve for it.

But to make things more manageable, we break lateral earth pressure down into three main types:

1. At-rest Earth pressures

2. Active Earth Pressure

3. Passive Earth Pressure

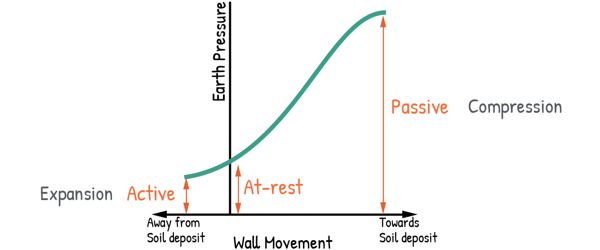
At-rest Earth Pressure

When a retaining wall is completely rigid — meaning it doesn’t tilt, slide, or deform — it holds the soil in place, preventing it from expanding outward or being compressed inward. In this condition, the horizontal stresses in the soil remain in equilibrium. The lateral pressure acting on the wall in this state is called At-rest Earth Pressure.

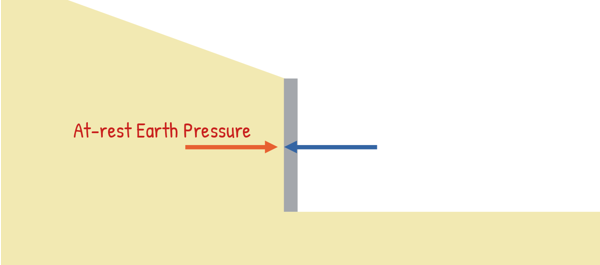
Active Earth Pressure

Unlike the at-rest condition, where the wall is rigid, here the wall actually moves — just a little. This movement can happen for many reasons—vibrations from traffic, erosion of soil behind the wall, temperature changes causing the wall material to expand or contract, poor construction, or even the swelling and shrinking of clayey soil.

Now, as the wall moves away from the soil, the soil right next to it wants to separate from the rest of the mass. But soil has shear strength, which resists this movement and holds it together. The wall doesn’t actually move this much—this is just exaggerated for a better view. In reality, it stays in contact with the soil. As now soil begins to hold itself together, the lateral pressure acting on the wall starts to decrease.

If the wall keeps moving, a point comes where the soil's full shear strength is completely reached. Beyond this point, the soil can no longer hold its shape—it fails along a slip surface. At this moment, the pressure on the wall is at its minimum. This lowest possible lateral pressure acting on the wall is called Active Earth Pressure.

Passive Earth Pressure

It is basically the opposite of Active Earth Pressure.

This time, instead of the wall moving away from the soil, it moves toward it, compressing the soil against itself. The soil resists this movement due to its shear strength, which pushes back against the wall. As a result, the horizontal pressure acting on the wall keeps increasing.

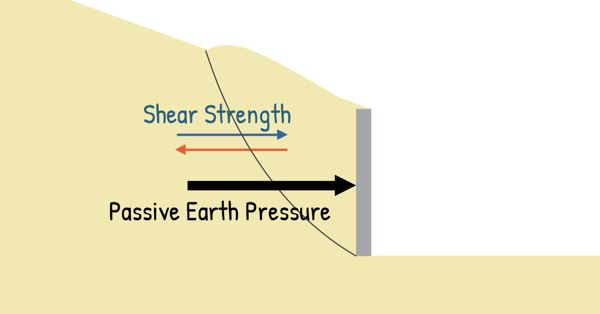
If the wall keeps pushing into the soil, a point comes where the soil's shear strength is completely used up. At this stage, the soil can no longer resist—it fails. And at this moment, the pressure on the wall is at its maximum. This highest possible lateral pressure acting on the wall is called Passive Earth Pressure.

So, in simple terms, Active Earth Pressure is the minimum lateral pressure a wall can experience, while Passive Earth Pressure is the maximum. In both cases, the soil is at the point of failure—either because it's expanding and breaking apart (Active) or getting compressed to its limit (Passive).

So, we now understand the different types of earth pressure—At-rest, Active, and Passive. But the big question is: How do we actually calculate these pressures?

Well, one of the simplest and most widely used methods was given by a a clever engineer from Scotland William John Macquorn Rankine. We just call it Rankine’s Theory.

Some people also pronounce it as Rank-eye-n, but the more common pronunciation—especially in engineering circles—is "RANK-in".

Assumption of Rankine's Earth Pressure Theory

Now, Rankine made a few assumptions to simplify the calculation of the Earth pressure.

1. He considered the soil to be perfectly elastic and homogeneous, meaning its properties are the same everywhere.

2. He also assumed the retaining wall is smooth—so no friction between the wall and the soil.

3. He worked with dry, cohesionless soil.

4. He assumed the soil surface behind the wall is perfectly level, not sloped, so the stress distribution remains uniform.

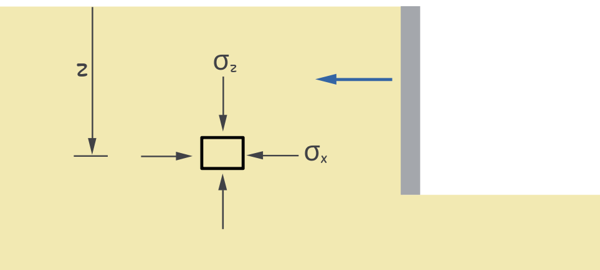
Now, Imagine a tiny element of soil at some depth z. This little guy is under two types of stress:

• Vertical stress (σ_z) from the weight of the soil above it.

• Horizontal stress (σ_x) from the surrounding soil pushing in.

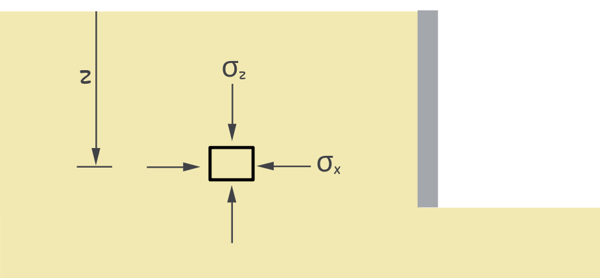
The vertical stress (σ_z) on this soil element is simply due to the weight of the soil above it. And since weight is just unit weight of soil (γ) multiplied by depth (z) of it, we can write it as:

σ_z = γ z

Since no shear stresses act on these horizontal and vertical planes, σ_z and σ_x are the principal stresses, and we initially assume σ_z as the major principal stress (σ?) and σ_x as the minor principal stress (σ?). But keep in mind—this is just an assumption!

In most natural soil conditions, vertical stress (σ_z) is usually greater than horizontal stress (σ_x)—makes sense, right? The weight of all the soil above is pressing down more than the sideways push from the surrounding soil.

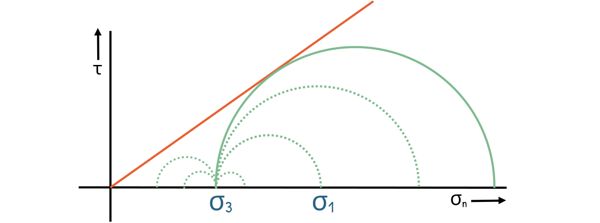
Now, we can actually visualize these stresses using a Mohr circle — which is a very useful way of representing stress conditions.

To understand the concepts of Principle stresses and Mohr circle take a look at the shear strength post. We discussed these in a little detail there.

We mark these stresses on the graph and plot the Mohr circle. Now, when the wall moves away from the soil, the horizontal stress (σ_x) starts decreasing. If the wall keeps moving away, σ_x keeps reducing until it officially becomes the minor principal stress (σ?), while the vertical stress (σ_z) takes over as the major principal stress (σ?).

With this, the Mohr circle keeps growing, and when the stress reaches the point where the soil is about to fail, the Mohr circle touches the failure envelope — which is basically the soil's strength limit. At this stage, the soil mass is said to be in the Active Rankine State.

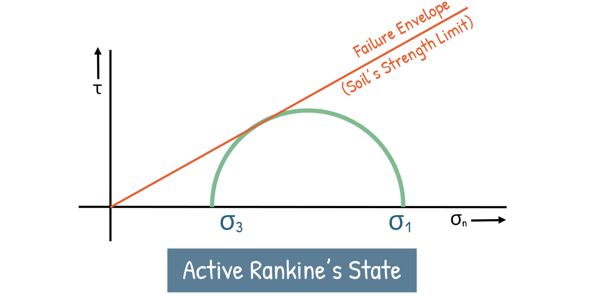
We know that the slope of the failure envelope is written as Φ — this represents the internal friction between soil particles.

Now, if we look at the triangle formed by the failure envelope, the stress axis and radius of Mohr circle,

we can write:

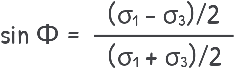
Solving for σ?, we get:

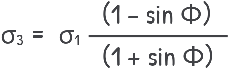
Here, σ? represents the active lateral pressure at failure which is denoted as P_a, and σ? is just the vertical stress, which we already defined as γz. The term (1 - sin Φ) / (1 + sin Φ) is commonly written as Ka, which is called the coefficient of active earth pressure.

So, putting it all together we get the expression for calculating the lateral earth pressure on soil in active condition:

Now, just like we did for Active Earth Pressure, let’s analyze what happens to a small soil element at depth z when the wall is pushing into the soil.

Again, the soil element experiences similar two stresses—Vertical stress (σ_z) due to the weight of the soil above it and Horizontal stress (σ_x) due to the surrounding soil pressure.

We can again draw the Mohr circle for this condition.

But this time, as the wall pushes into the soil, the horizontal stress (σ_x) increases. If this increase continues, σ_x eventually becomes greater than the vertical stress and takes the role of the major principal stress (σ?). Meanwhile, σ_z becomes the minor principal stress (σ?)—even though its value hasn’t changed, it’s now the smaller of the two.

With this increasing horizontal stress, the Mohr Circle grows. And if the compression keeps going to the point of failure, the Mohr Circle touches the failure envelope—marking the moment when the soil reaches its Passive Rankine State.

Now, if we look at the triangle formed by the failure envelope, the stress axis and the radius of the Mohr circle,

we can write:

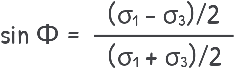
this time solving for σ₁, as this is the horizontal pressure, we get:

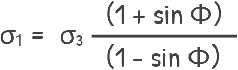
In this case, σ? corresponds to the Passive lateral pressure at failure, which we denote as Pp. σ? is the vertical stress (γz). The ratio (1 + sin Φ) / (1 - sin Φ) is called Kp, the coefficient of passive earth pressure.

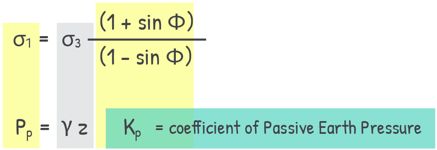
So, we can now express the lateral earth pressure in the passive state as:

Limitations of the Rankine's Theory :

1. While Rankine’s theory is simple and effective, it makes a few assumptions that may not always match real-world conditions. For example, theory assumes soil surface is level behind the wall, but If the soil behind the wall is sloped, it changes the pressure distribution.

2. The theory assumes the surface of the walls as smooth, but in reality, walls aren’t perfectly smooth. Rough walls increase friction, reducing active pressure and increasing passive pressure, so engineers add a wall friction factor.

3. Rankine’s theory assumes dry, cohesionless soil, but in wet conditions, hydrostatic pressure increases lateral pressure, and drainage systems may be needed.

4. While Rankine’s theory is for cohesionless soils only. But it was extended for cohesive soils also, where the failure envelope includes a cohesion intercept which was zero for cohesionless soils.

So, next time you see a retaining wall on a mountain road or anywhere holding back soil, you'll know exactly how much thought and engineering went into making sure it stays stable and safe. It's not simply a pile of concrete; it’s carefully designed to handle the forces of the earth behind it.