When heavy buildings or structures are built on the ground, they can make the ground compress a little over time due to their weight. This compression of soil, caused by factors like the weight of the building, is known as Settlement of soil. It has been described in detail in our previous post.

We also outlined in that post that total settlement of the soil has primarily three components.

1. Immediate Settlement

2. Consolidation Settlement or Primary Consolidation

3. Creep Settlement or Secondary Consolidation

The Total Settlement of soil is the sum of all three factors

We mentioned that Consolidation Settlement is the most dominant factor of the total settlement. Understanding and predicting the larger settlements that occur during primary consolidation is critical for safe and stable design.

Consolidation settlement, in particular, refers to the settlement of soil that occurs because of the dissipation of excess pore water pressure in saturated soils. It begins when a load is applied to the soil, such as the weight of a structure or an increase in the groundwater level. The soil particles begin to rearrange to bear this addition stress. This traps water in the voids between particles and causes a temporary rise in pore water pressure. Over time, this excess pressure dissipates as water slowly drains out, allowing the soil particles to settle closer together. This gradual compression of the soil due to water drainage is what we call consolidation settlement.

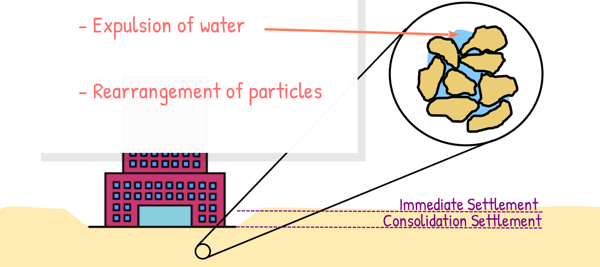
The introduction of Consolidation settlement has already been demonstrated in our previous post.

Consolidation is a time-dependent process, meaning that settlement continues over an extended period as the pore water pressure gradually dissipates and the soil mass continues to rearrange.

Consolidation settlement is more prominent in fine-grained soils like clay because water experiences difficulty flowing through their tiny, poorly connected pores resulting in very long time of consolidation.. Conversely, coarse-grained soils like sand or gravel consolidate quickly because of their high permeability that allows water to escape easily. Therefore, we study consolidation process primarily in fine-grained soils as both magnitude and time of settlement is significant in them.

The process of Primary Consolidation or Consolidation Settlement and the mechanics behind it can be explained with a very well known Spring Analogy given by Terzaghi.

Spring Analogy

Terzaghi demonstrated with the help of mechanistic model, the process of consolidation and the factors controlling the phenomenon.

The model consists of a cylindrical container filled with water. Inside, multiple pistons with perforations are stacked one above the other. Springs are placed between each piston. Piezometers (pressure gauges) are placed at the centre of each compartment to measure water pressure.

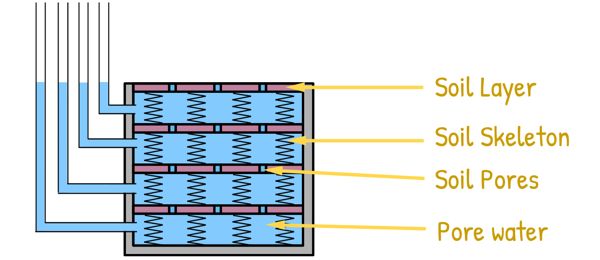
In this arrangement pistons represent soil layers. Springs depict the soil skeleton or arrangement of soil particles in the mass. Perforations in the pistons symbolize soil pores. And water is simply the pore water.

When a load is applied to the top piston, water cannot escape instantly through the perforations. The springs remain at their initial length as they cannot carry load until compressed. Therefore, the entire load is initially taken up by water, creating excess pore water pressure. The water in all the piezometric tubes rises to the same elevation above the original water level in the vessel. It is called excess pore water pressure because it is in excess of the original hydrostatic pressure.

After some time, water starts flowing progressively through the perforations, beginning from the top compartment. The amount of water in the lower compartments remains unchanged initially. As water flows out of the upper compartments, their volume decreases, and the springs begin to compress. This signifies that the springs start carrying a portion of the applied load, and the excess pore water pressure reduces correspondingly.

With further time, water migrates from the lower compartments too, leading to a gradual dissipation of excess pore water pressure throughout the system and simultaneous compression of the springs. Finally, after a very long time, this flow stops, and equilibrium is reached. Excess pore water pressure everywhere becomes zero, and the entire load is carried by the compressed springs. This signifies the end of consolidation settlement., with the system reaching a more stable, densified state.

This whole process simulates the consolidation of soils, particularly clay soils. Though Terzaghi's spring analogy has some limitations like real soil is not perfectly elastic like springs but it provides a valuable conceptual understanding of consolidation settlement in saturated clays.

When a constant static load, like the weight of a building (represented by Δσ), is applied to saturated soil, it behaves similar to that of the Terzaghi’s spring analogy model. The soil particles act like the springs, and the water filling the spaces between particles is analogous to the water in the cylinder.

Just like the piezometer measures water pressure in the analogy, pore water pressure (u) acts similarly in the soil. The pressure carried by the springs is analogous to the effective stress σ’ developed in the soil. Effective Stress is the internal force that the soil structure, the arrangement of soil particles, can withstand without collapsing.

Generally, a load or pressure increment Δσ, applied to the saturated soil, is shared by both solid particles and water. We can write total stress applied as sum of pressure supported by soil as effective stress acting on particles and pressure supported by water as pore water pressure

Δσ’ + Δu = Δσ

Δσ = change in Total Stress

Δu = change in Pore water pressure

Δσ’ = change in Effective Stress

We expressed all the quantities as change in their values because before applying the additional stress Δσ, there existed a load of particles self weight and weight of water which soil particles were already supporting. Also because of that there was some water pressure in the pores.

But initially, just after the application of pressure, the entire load is taken by water, which cause to increase in the water pressure which is known as the excess pore water pressure, Δu. Since no pressure is taken up by soil particles at this moment, the change in effective stress is zero.

So we can write

0 + Δu = Δσ

also that at t = 0, excess pore water pressure is equal to the total stress applied to the soil.

Δu = Δσ

This excess pore water pressure creates a hydraulic gradient and water gradually begins to flow out of the soil. As water slowly drains through the soil pores the excess pore water pressure reduces and the applied pressure is transferred from the water to the solids, increasing the effective stress.

Eventually, after a long time, all the excess pore water pressure dissipates (Δu = 0), and the entire applied load is supported by the soil structure as effective stress

Δσ' + 0 = Δσ

so effective stress become total stress applied on soil.

Δσ' = Δσ

As water drains out of the soil pores and effective stress on particles increases, the soil particles gradually compact and settle, leading to a reduction in the volume of the soil mass. And that is consolidation.

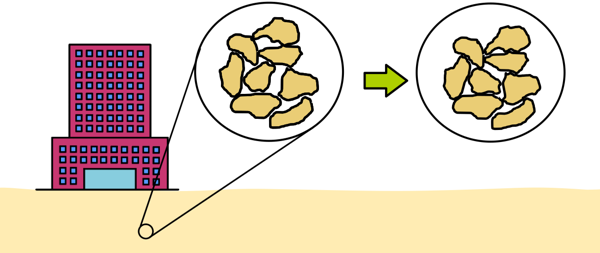
Decrease in volume of soil is generally expressed as change in void ratio. We will study more about consolidation and change in void ratio with time and many other related things in coming posts.