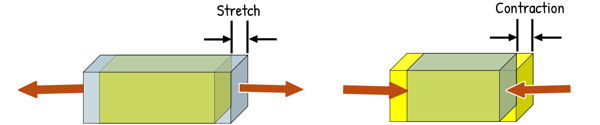
When a force acts on an object, particularly along its length, it either stretches or shortens the object. But can we precisely determine how much it stretched or shortened?
That is exactly what we are going to explore in this post. We’ll look at axial loads and their measurable effects, learn how to calculate deformation using a simple but powerful formula, and see how to handle bars with varying cross-sections or materials — a common situation in real-world structures.
An axis is simply an imaginary straight line that helps us define direction along a body’s geometry.
For any structural member like a rod or a beam, we mainly care about three key axes.
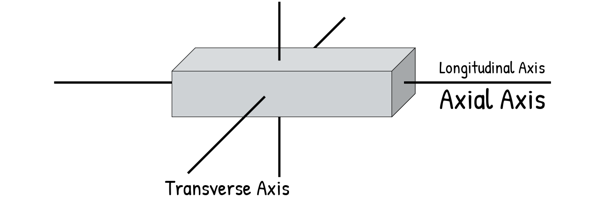
The axis that runs along the length of the member, is called Longitudinal axis or the Axial axis. The other two axes, perpendicular to the axial axis, are called Transverse axes.
Now, when a force acts along this axial axis, we call it an Axial load. This axial force can do one of two things: it can either try to push the body inwards or pull it outwards.
- A pushing axial force compresses the body. We call this a Compressive force, and it results in a shortening of the body’s length.
- Conversely, a pulling axial force stretches the body. This is a Tensile force, and it causes the body’s length to increase.
Now, when we actually try to figure out how much a body has stretched or shortened, we have to bring in some math — a weapon for precision. And to keep the calculations clear, we follow a sign convention: we usually take tensile forces and the elongation as positive, and compressive forces and the shortening as negative.
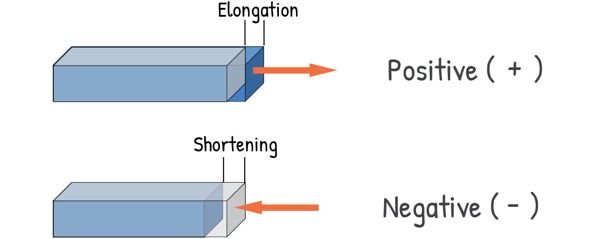
Of course we can take tensile force as negative and compressive force as positive and the final physical result won’t change. But it is just a convention that every follows and it makes easier for other person to understand when he or she looks at your calculations.
But once we stick to any convention, we must keep it till end. Because later we will see both compressive and tensile forces acting on the same object, keeping these signs straight will not only make your life easier but also prevent costly mistakes.
So we come back to our question : How much does an object actually stretch or shorten under these axial forces?
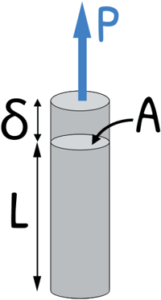
For that, let’s consider a metal rod of length L and cross-sectional area as A. A tensile force P is pulling the rod axially. As a result the rod has stretched by some amount say δ. Our purpose here is to know this δ.
We begin with the stress generated in the body because of the applied force and which is given as axial force over the cross-sectional area over which it is acting.
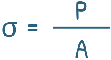
This stress causes the material to deform. And the amount of deformation, relative to its original length, is called strain. Which we write as this

We have discussed all these in detail in our previous post.
We also discussed there the Hooke’s law, that connects stress with strain generated in a material when external load applied to it. The Hooke’s law suggest this relationship:
σ = Eε
here E is the Modulus of Elasticity, which is also called Young’s Modulus. It’s a property of the material that tells us how strongly it resists being stretched or compressed. Higher the Young’s modulus more resistant it is to deformation.
Now, we already have expression for σ and ε let’s substitute them into Hooke’s Law:
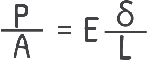
solving this, we get the value of δ
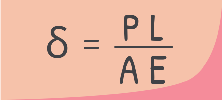
That’s our formula — a clean, powerful way to calculate how much an object stretches or shortens under an axial load.
Let’s quickly appreciate what this formula tells us:
- The change in length delta (δ) is directly proportional to the applied force (P) – more force, more stretch.
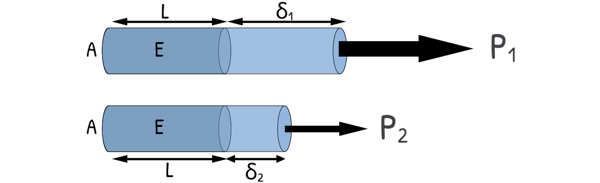
- It’s also directly proportional to the original length (L). A longer bar will stretch more than a shorter one under the same force.
- But it’s inversely proportional to the cross-sectional area (A), that means a thicker bar will deform less because the force is spread over a larger area.
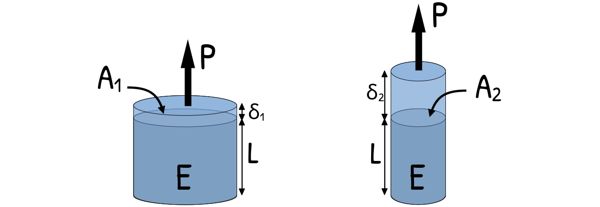
- And finally, it’s inversely proportional to E. This E represents how stiff the material is.
Steel, for example, has a very high E, so it resists deformation — it barely stretches.
Rubber, on the other hand, has a very low E, so it deforms easily, even under small loads.
We need to keep in mind that Hooke’s law is only valid for certain conditions. Hence the formula of deformation we just derived will also obey those conditions. Those conditions are assumptions that
- The material must be homogeneous, meaning it has the same properties throughout. Think of a pure block of steel – it’s the same everywhere. We’re not dealing with something that suddenly changes composition.

- It must be isotropic — its properties should be the same in every direction. It is clear with the example of a piece of wood is often not isotropic. Its properties are different along the grains and perpendicular to the grains.

- The material must behave elastically and linearly — that is, stress should be directly proportional to strain, and it should return to its original shape when the load is removed.
- The deformations must be small. If an object stretches by a huge amount, its geometry changes significantly, and our initial assumptions, like constant cross-sectional area, might no longer hold true.
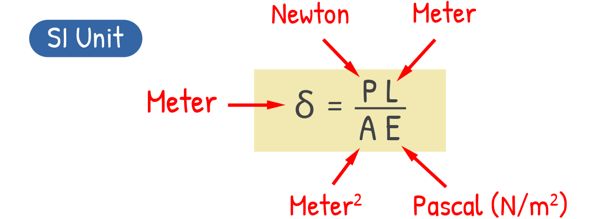
One quick note on units: if we use SI units — newtons for force, meters for length and area, and pascals (or newtons per square meter) for Young’s Modulus — the deformation δ will come out in meters.
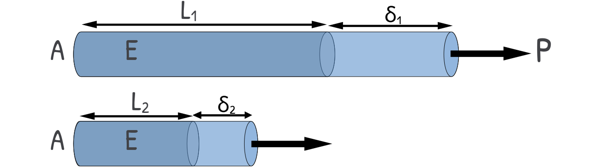
But in real-world structures, bars and materials are rarely uniform throughout. What if the bar has different thicknesses along its length? What if it is made up of different materials welded together, each with a different stiffness?

For such cases, we treat the bar as a series of individual segments and apply our deformation formula to each segment separately. Each segment will have its own length (Li), cross-sectional area (Ai), and possibly material properties (Ei).
For each segment, we calculate the deformation as this:

and so on…
And the total deformation of the entire bar is simply the sum of all segment deformations:
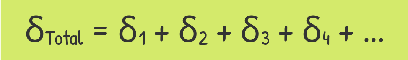
The concepts we’ve explored today are very essential for understanding how materials respond to forces. We now have the tools to calculate how much a simple bar, or even a stepped one, will deform under an axial load.
But the story of deformation doesn’t end here! In our very next post, we’ll introduce another powerful factor: thermal expansion.