Have you ever wondered what happens inside materials when you push, pull, or even just sit on something?
When a force or pressure is applied to a material, it tries to change material’s shape – we call this Deformation.
But the material doesn’t just allow this to happen, at least not easily! They resist deformation by developing internal forces — we can think of this as an internal resistance that pushes back against the applied load. This internal resistance is called Stress. Or even more precisely, stress is defined as the force divided by the area over which it acts.
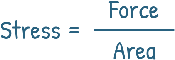
It’s usually denoted by the Greek letter sigma: σ
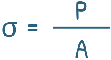
In SI units, stress is measured in Newton per square meter (N/m2) — or pascals (Pa). One pascal is one newton per square meter.
But even though the material resists the deformation caused by external force, no real-world material is perfectly rigid. So under that applied force, there will always be some change in the material’s shape or size. The amount of that deformation, relative to the material’s original size, is called strain.
It’s defined as the ratio of the change in dimension to the original dimension.

It’s usually denoted by the Greek letter epsilon: ε.
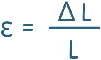
ΔL is the change in length
Since it’s a ratio of two lengths, strain has no units — it’s dimensionless. It simply tells us how much the material stretches or compresses compared to where it started.
Now, both stress and strain are of different types.
Stress is commonly categorized as normal stress, shear stress, bearing stress, bending stress, and torsional stress — depending on how the force is applied.
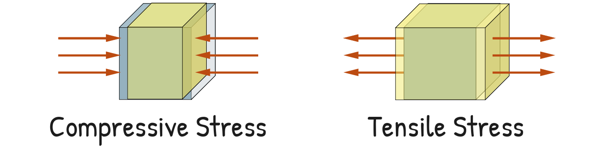
When an external force tries to pull or push on a material, the internal forces resisting this act perpendicular to the material’s cross-section – this is Normal Stress.
The pushing force brings compression in the material which leads to development of Compressive Stress. While the pulling force brings tension in the material and develops Tensile Stress.
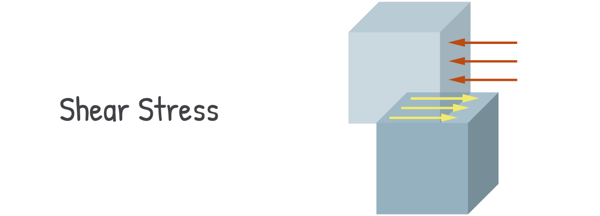
If the external force tries to slide one part of the material past another, the internal forces resisting this act parallel to the cross-section – this is Shear Stress.
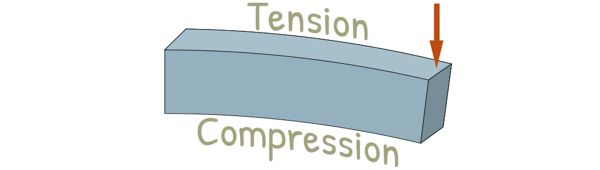
We also see Bending Stress develop when a force tries to bend or curve a material, creating internal tension on one side and compression on the other.
And a twisting force generates Torsional Stress, which is essentially shear stress acting around the axis of the twist.
Depending on the type of stress developed, a corresponding type of strain is produced in the body. We typically categorize strain as tensile strain, compressive strain, volumetric strain, or shear strain, based on how the material deforms.
We should note that, stress in a material induces strain but opposite is equally true. That is, when a body is strained, stresses generate in to it.

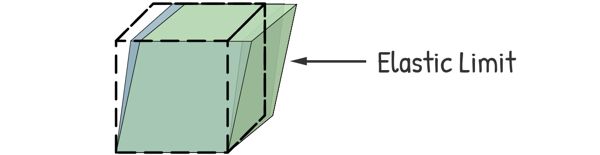
Now we know that, when a material is subjected to an external force, it deforms — it changes shape or size. But if we remove that force and the material returns to its original shape and size, we call it an elastic body.
But the thing is, recovery only happens if the deformation is within a certain limit. Go beyond that limit, and the material may never return to its original shape. That limit is called the elastic limit. And the ability of a material to regain its original form after the force is removed is known as elasticity.
A classic example is a rubber band — stretch it, and it springs back when released.
So, how do stress and strain relate in that elastic region? This relationship is described by Hooke’s Law.
Hooke’s Law states that when a material is loaded within its elastic limit, the stress generated in the body is directly proportional to the strain produced.
Stress ∝ Strain
This means as the stress in the body increases, strain increases with it in a linear, predictable way, till it is in the elastic limit.
Mathematically, this proportionality means that the ratio of stress to its corresponding strain is a constant value within this elastic region.
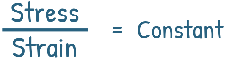
This constant is incredibly important and is known as the Modulus of Elasticity or Young’s Modulus, and it’s denoted by E

It is also called Modulus of Rigidity or Elastic Modulii.
Just remember — Hooke’s Law is only valid as long as the stress and strain are within the elastic limit. Once that limit is crossed, the stress-strain relationship is no longer linear, and the material starts behaving differently and deforms permanently.
We can even plot a graph to visualize how stress and strain develop in a material as we apply force to it. This is called a stress-strain diagram.
On this graph, the horizontal axis represents strain — how much the material deforms. The vertical axis shows stress — the internal resistance the material develops.
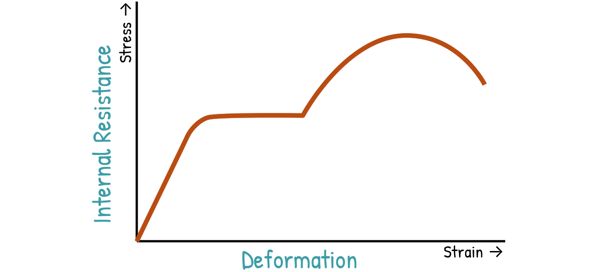
As we gradually increase the applied load, tracing the stress and the resulting strain gives us a curve that reveals the material’s behaviour.
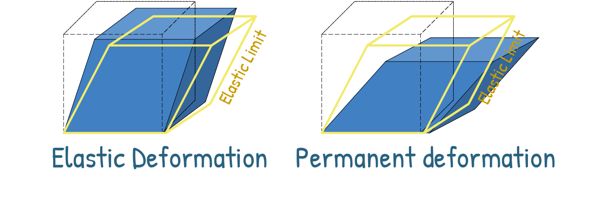
Right at the beginning of the graph, we see a straight line. This is known as the elastic region, and it is where the Hooke’s Law applies — stress is directly proportional to strain.
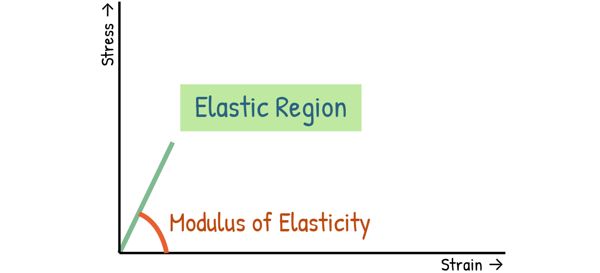
If we remove the external force while the material is in this region, it will spring back completely to its original shape, with no permanent deformation.
The slope of this line gives us the modulus of elasticity, or Young’s modulus.
If the slope of this line is higher, meaning it’s steeper, we get a higher value for Young’s Modulus. A steeper line shows that even a large increase in stress results in only a small amount of strain. This tells us the material is strong or stiff – it resists deformation strongly in the elastic region.
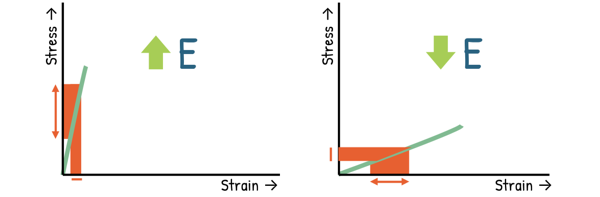
Conversely, a gentle slope means a lower Young’s Modulus. This indicates that even a slight increase in stress causes a much larger strain or deformation. That means, these materials are more flexible or less stiff.
Hence, the value of Young’s Modulus tells us about the property of the material that how stiff or flexible it is. The larger the value of E, the harder it is to stretch or compress the material.
Now, in our stress-strain graph, the point where the straight line ends is called the Proportional limit.
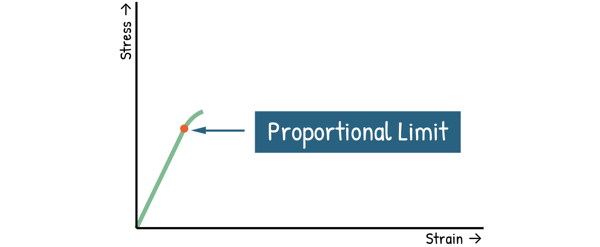
It’s the point beyond which Hooke’s Law no longer valid. Stress and strain are no longer related to each other linearly, but still the material may return to its shape when the external force is removed.
Next, we hit the Elastic Limit.

This is the critical point beyond which deformation is no longer fully reversible. If you increase the stress past the elastic limit, the material starts to deform permanently, and this permanent change is called plastic deformation.
Then, we reach the yield point — This is where the material undergoes a noticeable increase in strain (deformation) even with little or no increase in stress. For many materials, this is visible as a flat region in the curve, called the yielding region. Here, the material stretches without much increase in stress.

As we keep increasing the load, the stress in the material continues to rise until it reaches the Ultimate stress — also called Ultimate strength. This is the maximum stress the material can handle before it starts to fail.
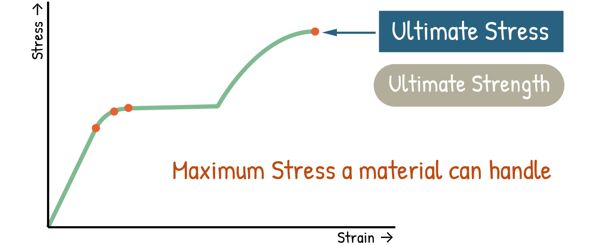
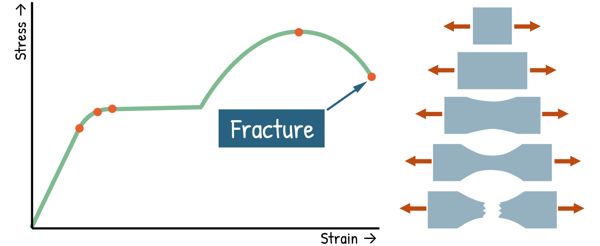
After that, even though the material keeps stretching, it starts losing its ability to carry load — the graph begins to drop. This is where the material starts to form a neck — a localized reduction in cross-sectional area. It continues to stretch at that narrowed spot until, we reach the breaking point — also known as the fracture point — where the material fails and breaks.
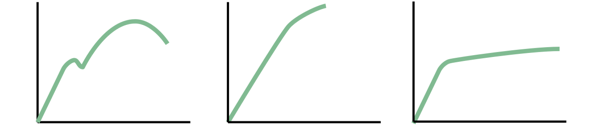
Different materials have different stress-strain curves — steel, rubber, plastic — each one tells a different story of strength, flexibility, and failure.
So whether you’re designing bridges, testing new materials, or just curious about what makes things strong — understanding stress and strain is your first step into the world of material strength.