A dam is a barrier that restricts the flow of water and can be used to collect the water and this water may be utilized for many purposes.

A Dam can be constructed using different kinds of materials.

In earth dams the construction material is rocks and soil. The water that the dam holds flows from upstream through the voids present in the soil of the body of the dam to downstream by the action of hydraulic head difference. This phenomenon of movement of water through the soil is called seepage.

We have already determined the quantity of seepage through the body of an earth dam with a horizontal filter at its downstream. Here we will discuss the shape of the phreatic line in an earth dam when no filter is provided and seepage water exists from the downstream face of the dam.

let's assume an earth dam that retains the water up to the height h. We also assume that foundation of the dam is impermeable and water will only seep through the body of the dam. We know seepage through an earth dam is the case of unconfined flow of which the upper boundary is not known, which is the top flow line.

Casagrande observed that the shape of this top flow line, which is also called phreatic line, is close to the basic parabola for most of its length. So he recommended it can also be taken as basic parabola with necessary corrections at the upstream and downstream faces manually so that it conforms to basic conditions of the flow net, such as flow line should be perpendicular to the equipotential line.

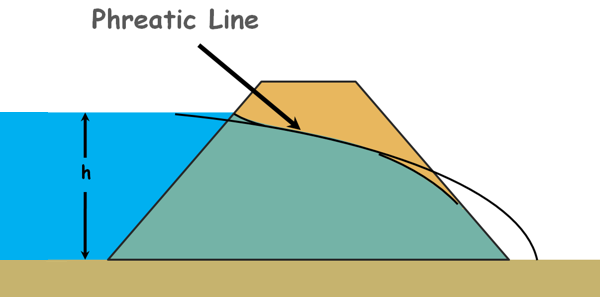
So to obtain the phreatic line first we need to draw the base parabola and for that we take the downstream point of the dam as the focus F of the parabola and also the origin. Also we name few points in the diagram.

Casagrande also recommends that this seepage parabola curve starts from a point, say point H, on the upstream. If we take the horizontal projection of the wet upstream face of the dam on the water surface as GI, then the distance of this point H from the point G on the face of the dam, GH is given as 0.3 times GI.

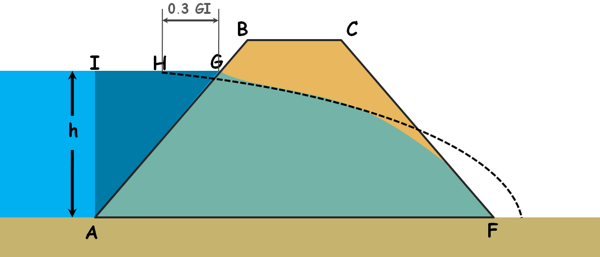
Now we can obtain the parabola’s directrix using the property of the parabola that states, the distance of any point on the parabola from the directrix and its focus is equal. Point H is on the parabola and F is the focus of the parabola. Distance of this point H from the focus and parabola’s directrix should be equal.

So to obtain the directrix we extend the upstream water level and using the compass of length HF make an arc that cuts this extension. From this point we draw a perpendicular to the base of the dam and we get our directrix.

Then we determine the intermediate points of the curve using the same parabola property. We join all those points to find our base parabola.

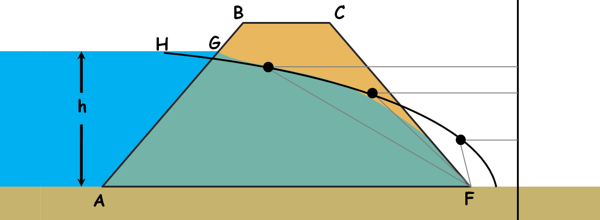
Now to draw the phreatic line from this parabola we will have to make some corrections.

For the correction at the upstream we draw a perpendicular line to the upstream face AB at point G, from where the top flow line originates and gradually blend it into the parabola curve manually.

For the correction at the downstream we need to understand few things. When horizontal filter is not provided the seepage line cuts the downstream face of the dam and the downstream face acts as the discharge face.

We usually do not permit this to happen because when the seepage water exits from the downstream face of the dam it may carry away the dam material with it, which may cause to create pipe like openings. This phenomenon, called piping, may cause the failure of the downstream slope or the whole dam.

The downstream face of the dam is inclined with horizontal. This inclination of the discharge face is described relative to the bottom boundary flow line as angle β and is measured clockwise.

In case of the horizontal filter, the angle between bottom flow line and discharge face is this and β is 180⁰.

In case of discharge face being a rock toe this angle β is greater than 90⁰.

In case of discharge face being the downstream face the angle β will be less than 90⁰.

Phreatic line meets differently to the different types of discharge faces.

When β is 180⁰ phreatic line meets the discharge face exactly as the base parabola.

When β is greater than 90⁰ phreatic drops vertically on the discharge face.

When β is less than 90⁰ the phreatic line meets the discharge face tangentially and extends towards the toe of the dam.

So in both of the last two cases an additional correction at exit is required.

When β is less than 90⁰ the basic parabola goes outside the downstream face. Let’s say the base parabola cuts the dam at the downstream at some point J and meet the horizontal at point K.

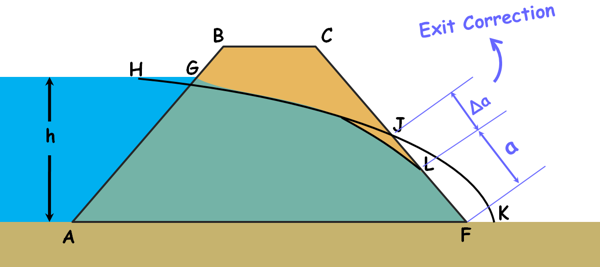
The actual phreatic line in this case curves to meet the downstream discharge face tangentially at some point say L below the point J.

The deviation JL is the distance by which the basic parabola has to be shifted to obtain the actual phreatic line. It is called the exit correction and it is denoted as Δa. And the distance JF is written as a + Δa.

But how do we know how much we have to shift the parabola. What is the value of Δa.

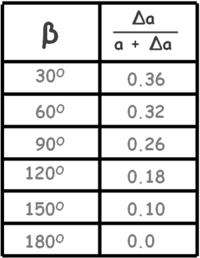
Well, Casagrande observed this Δa varies with the downstream slope angle β. So he gave a chart for the exit correction Δa the distance by which the basic parabola is shifted to locate the point where the actual seepage line cuts the discharge face.

In the chart we can notice that the exit correction Δa is zero when the angle β is 180⁰. If we remember we also did not have to apply the exit correction in the case of horizontal filter.

Once we obtain Δa an arc of Δa length is cut on the downstream face and the base parabola curve is joined at this point to obtain the actual phreatic line.

So this is how we create the phreatic line for an earth dam when seepage water exits from the downstream face of the dam.

We should keep in mind that this chart is applicable only when the downstream slope angle β is greater than or equal to 30⁰ (β >= 30⁰).

Now Let’s try to estimate the seepage through an earth dam with discharge angle less than 30⁰

Let us consider any section of the flow and name it PQ.

As we know the flow of free water through the soil is governed by the Darcy’s law, we can write discharge through this section as

k is the permeability of the dam material.

A is area of the cross-section through which seepage water is passing.

And i is the hydraulic gradient with which water is flowing through this section.

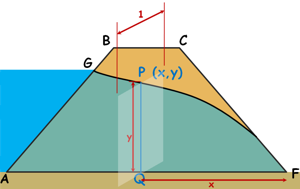
Say co-ordinates of point P is x,y then height of this section which is at distance x from origin is y. lets calculate the discharge for unit width of the dam. So area of this section can be written as this

Let’s say a slight distance dx away from this section we observe a head difference of dy. So hydraulic gradient causing the flow at this section can be written as change in head over the distance over which the change occurred.

According to Dupuit’s assumption, hydarulic gradient for a dam having discharge face angle less than 30⁰ is equal to the dy/dx. So we assume that the hydraulic gradient is same at all the locations throughout the dam. Which means for β < 30⁰ the length of the flow becomes so long that it roughly becomes a straight line with uniform gradient.

So we can write discharge through this section as this

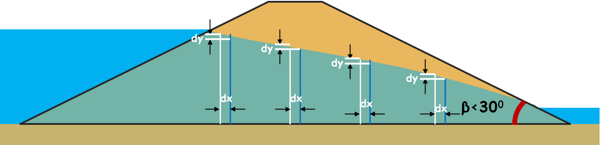
We can see, discharge through any section of the dam is equal to the discharge through the section where the phreatic line touches the downstream face because whatever amount of water coming from any section is going through this section as foundation is impermeable. At this section because of the geometry it is easier to determine the value of hydraulic gradient and height of the cross-section.

now from the triangle RSF height of section RS, that is y, can be written as asin β

Now at dx distance away from this section change in head is dy. So by this triangle we can determine the value of dy and dx as zsinβ and zcos β

dy = zsinβ

dx = zcos β

So Hydraulic gradient can be written as

i = sin β/cos β = tan β

So discharge though this section can be written as

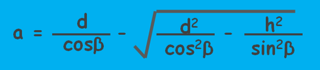
Now in this equation only unknown is a and once we know the a we can calculate the discharge through the dam. a can be find out by equating the discharge through any section of the dam and discharge through the section RS of the dam.

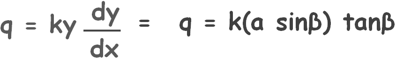
By integrating and applying simple mathematics we arrive at a very simple equation which gives the value of a.

Now let’s try to estimate the seepage through an earth dam with discharge angle greater than 30⁰ but less than 60⁰

No we will attempt no such dangerous task.

But one thing to remember is that when β was less than 30⁰ we calculated discharge through the dam using Dupuit’s assumption that hydraulic gradient will be dy/dx.

But when β is greater than 30⁰ and less than 60⁰ Casagrande suggested that hydraulic gradient is given by

where distance s is measured along the curve.

Again After some easy calculations we find the discharge through the dam as this

and the value of a in this case as this

To arrive at these equations we use some approximations and for discharge angles greater than 60⁰ the error because of those approximations becomes large. So we do not use this method for β greater than 60⁰.

But one important thing to notice here is that in both the cases of the value of “a” that is distance of exit point of the seepage line from the toe of the dam at the discharge face does not depend on amount of seepage discharge. It is completely dependent on the geometry of the downstream slope.